Temas Selectos de Econofísica: Modelado de agentes económicos con Python.¶

Licenciatura en Física

Facultad de Ciencias

UABC, Agosto-Diciembre 2025

Instructor: Dr. Andrés García Medina

email: andgarm.n@gmail.com

sitio: https://sites.google.com/view/andresgm/home.

Actividad: Implementación de Modelo de la distribución de la riqueza con MESA¶

Este cuaderno adapta fragmentos de código y documentación del proyecto Mesa con fines educativos.

Código original: https://github.com/projectmesa/mesa

Descripción del Modelo¶

  • Este es un modelo simulado de una economía basada en agentes.

  • En una economía basada en agentes, se estudia el comportamiento de un agente económico individual, como un consumidor o productor, en un entorno de mercado.

  • Este modelo fue propuesto por Dragulescu, A., & Yakovenko, V. M. (2000). Statistical mechanics of money. The European Physical Journal B-Condensed Matter and Complex Systems, 17, 723-729.

Las suposiciones que rigen este modelo son:

1. Existen un número determinado de agentes.
2. Todos los agentes comienzan con 1 unidad de dinero.
3. En cada paso del modelo, un agente le da 1 unidad de dinero a otro agente.

Dependencias¶

In [3]:
#pip install mesa
In [4]:
# Tiene una gran colección de funciones matemáticas para operar con estos arreglos.
import numpy as np

# Manipulación y análisis de datos.
import pandas as pd

# Herramientas para visualización de datos.
import seaborn as sns

# Modelización basada en agentes en Python
import mesa

Crear Agente¶

Primero, creamos el agente.

Contexto:

  • Los agentes son las entidades individuales que actúan en el modelo.
  • Mesa asigna automáticamente a cada agente creado un número entero como unique_id.

Información específica del modelo: Los agentes son los individuos que intercambian dinero, en este caso, la cantidad de dinero que un agente individual tiene se representa como riqueza.

Implementación del código:

  • Esto se realiza creando una nueva clase (u objeto) que extiende mesa.Agent, creando una subclase de la clase Agent de Mesa.
  • La nueva clase se llama MoneyAgent.
  • La clase MoneyAgent se crea con el siguiente código:
In [4]:
class MoneyAgent(mesa.Agent):
    """Un agente con riqueza inicial fija."""

    #Método constructor
    def __init__(self, model):
        # Pasar los parámetros de la clase padre.
        super().__init__(model)

        # Crear la variable del agente y establecer los valores iniciales.
        self.wealth = 1
In [4]:
#Si deseamos conocer todos los métodos heredados
dir(MoneyAgent)
Out[4]:
['__class__',
 '__delattr__',
 '__dict__',
 '__dir__',
 '__doc__',
 '__eq__',
 '__format__',
 '__ge__',
 '__getattribute__',
 '__getstate__',
 '__gt__',
 '__hash__',
 '__init__',
 '__init_subclass__',
 '__le__',
 '__lt__',
 '__module__',
 '__ne__',
 '__new__',
 '__reduce__',
 '__reduce_ex__',
 '__repr__',
 '__setattr__',
 '__sizeof__',
 '__str__',
 '__subclasshook__',
 '__weakref__',
 '_ids',
 'advance',
 'create_agents',
 'random',
 'remove',
 'rng',
 'step']
In [5]:
#Si deseamos saber que hace por ejemplo `step`:
help(MoneyAgent.step)

Help on function step in module mesa.agent:

step(self) -> 'None'
    A single step of the agent.
In [6]:
#Si queremos inspeccionar el codigo fuente:
import inspect

print(inspect.getsource(MoneyAgent.__init__))

    def __init__(self, model):
        # Pasar los parámetros a la clase padre.
        super().__init__(model)

        # Crear la variable del agente y establecer los valores iniciales.
        self.wealth = 1

Crear Modelo¶

  • La clase agente (población de objetos agente que hacen algo).
  • La clase modelo (un objeto modelo que gestiona la creación, activación, recolección de datos, etc., de los agentes).

Contexto: El modelo se puede visualizar como una lista que contiene todos los agentes. El modelo crea, mantiene y gestiona todos los objetos agente, específicamente en un diccionario. El modelo activa a los agentes en pasos de tiempo discretos.

Información específica del modelo: Cuando se crea un modelo, se especifica el número de agentes dentro del modelo. Luego, el modelo crea los agentes y los coloca en un conjunto de agentes.

Implementación del código: Esto se realiza creando una nueva clase (o objeto) que extiende mesa.Model y llama super().__init__(), creando una subclase de la clase Model de Mesa. La nueva clase se llama MoneyModel. Un punto crítico es que puedes usar el argumento seed para establecer una semilla que controle el generador de números aleatorios de la clase modelo, lo que permite la reproducibilidad de los resultados.

La clase MoneyModel se crea con el siguiente código:

In [5]:
class MoneyModel(mesa.Model):
    """Un modelo con un número determinado de agentes."""

    def __init__(self, n, seed=None):
        super().__init__(seed=seed)
        self.num_agents = n
        # Crear los agentes
        MoneyAgent.create_agents(model=self, n=n)

Activar a los agentes¶

Con los aspectos básicos de la clase Agente y la clase Modelo creados, ahora podemos activar a los agentes para que hagan cosas.

Contexto: La función do de Mesa llama a las funciones de los agentes para hacer crecer tu ABM. Un paso es la unidad más pequeña de tiempo en el modelo, y a menudo se le conoce como un tick. En cada paso del modelo, uno o más de los agentes -- generalmente todos ellos -- son activados y dan su propio paso, cambiando internamente y/o interactuando entre ellos o con el entorno.

Información específica del modelo:

Para esta sección, reordenaremos aleatoriamente el orden de activación de los agentes usando mesa.Agent.shuffle_do y haremos que la función step de los agentes imprima el unique_id que se les asignó durante el proceso de creación del agente.

Implementación del código:

Usando la convención estándar de ABM, agregamos una función step a la clase MoneyModel que llama a la función mesa.Agent.shuffle_do. Luego pasamos al shuffle_do el parámetro "step". Esto le dice a Mesa que busque y ejecute la función step en nuestra clase MoneyAgent.

In [6]:
class MoneyAgent(mesa.Agent):
    """Un agente con riqueza inicial fija."""

    def __init__(self, model):
        # Pasar los parámetros de la clase padre.
        super().__init__(model)

        # Crear el atributo del agente y establecer los valores iniciales.
        self.wealth = 1

    def say_hi(self):
        # Para fines de demostración, imprimiremos el unique_id del agente.
        print(f"Hola, soy un agente, puedes llamarme {self.unique_id!s}.")
In [25]:
class MoneyModel(mesa.Model):
    """Un modelo con un número determinado de agentes."""

    def __init__(self, n, seed=20):
        super().__init__(seed=seed)
        self.num_agents = n

        # Crear n agentes
        MoneyAgent.create_agents(model=self, n=n)

    def step(self):
        """Avanzar el modelo un paso."""
        # Esta función reorganiza de manera pseudo-aleatoria la lista de objetos agente y
        # luego itera llamando la función pasada como parámetro.
        self.agents.shuffle_do("say_hi")

Ejecutar el Modelo¶

Ahora tenemos las piezas de un modelo básico. El modelo se puede ejecutar creando un objeto de modelo y llamando al método step. El modelo se ejecutará por un paso e imprimirá el unique_id de cada agente. Puedes ejecutar el modelo durante múltiples pasos llamando al método step varias veces.

Crea el objeto del modelo y ejecútalo por un paso:

In [27]:
starter_model = MoneyModel(10)
starter_model.step()

Hola, soy un agente, puedes llamarme 6.
Hola, soy un agente, puedes llamarme 4.
Hola, soy un agente, puedes llamarme 1.
Hola, soy un agente, puedes llamarme 8.
Hola, soy un agente, puedes llamarme 9.
Hola, soy un agente, puedes llamarme 10.
Hola, soy un agente, puedes llamarme 7.
Hola, soy un agente, puedes llamarme 2.
Hola, soy un agente, puedes llamarme 5.
Hola, soy un agente, puedes llamarme 3.

Si ejecutamos este paso varias veces veremos que el orden de los agentes cambia

In [11]:
starter_model.step()

Hola, soy un agente, puedes llamarme 1.
Hola, soy un agente, puedes llamarme 7.
Hola, soy un agente, puedes llamarme 8.
Hola, soy un agente, puedes llamarme 2.
Hola, soy un agente, puedes llamarme 5.
Hola, soy un agente, puedes llamarme 10.
Hola, soy un agente, puedes llamarme 4.
Hola, soy un agente, puedes llamarme 3.
Hola, soy un agente, puedes llamarme 6.
Hola, soy un agente, puedes llamarme 9.

Actividad:¶

  • Cambia la semilla de None a un número como 42 y observa el impacto

  • Cambia shuffle_do a solo do y observa el impacto

Ejercicio¶

Modifica el código a continuación para que cada agente imprima su wealth cuando sea activado.

In [28]:
class MoneyAgent(mesa.Agent):
    """Un agente con riqueza inicial fija."""

    def __init__(self, model):
        # Pasar los parámetros a la clase padre.
        super().__init__(model)

        # Crear la variable del agente y establecer los valores iniciales.
        self.wealth = 1

    def say_wealth(self):
        # FIXME: Necesitamos imprimir la riqueza del agente
        print("¡Hola, soy un agente y estoy sin dinero!")

Crea un modelo con 12 agentes y ejecútalo durante unos pasos para ver la salida.

Solución¶

In [31]:
class MoneyAgent(mesa.Agent):
    """Un agente con riqueza inicial fija."""

    def __init__(self, model):
        # Pasar los parámetros a la clase padre.
        super().__init__(model)

        # Crear la variable del agente y establecer los valores iniciales.
        self.wealth = 1

    def say_wealth(self):
        # Imprimir la riqueza del agente
        print(f"¡Hola, soy un agente y tengo {self.wealth} de riqueza!")
In [32]:
class MoneyModel(mesa.Model):
    """Un modelo con un número determinado de agentes."""

    def __init__(self, n, seed=None):
        super().__init__(seed=seed)
        self.num_agents = n

        # Crear n agentes
        MoneyAgent.create_agents(model=self, n=n)

    def step(self):
        """Avanzar el modelo un paso."""
        # Esta función reorganiza de manera pseudo-aleatoria la lista de objetos agente y
        # luego itera llamando la función pasada como parámetro.
        self.agents.shuffle_do("say_wealth")
In [33]:
starter_model = MoneyModel(12)
starter_model.step()

¡Hola, soy un agente y tengo 1 de riqueza!
¡Hola, soy un agente y tengo 1 de riqueza!
¡Hola, soy un agente y tengo 1 de riqueza!
¡Hola, soy un agente y tengo 1 de riqueza!
¡Hola, soy un agente y tengo 1 de riqueza!
¡Hola, soy un agente y tengo 1 de riqueza!
¡Hola, soy un agente y tengo 1 de riqueza!
¡Hola, soy un agente y tengo 1 de riqueza!
¡Hola, soy un agente y tengo 1 de riqueza!
¡Hola, soy un agente y tengo 1 de riqueza!
¡Hola, soy un agente y tengo 1 de riqueza!
¡Hola, soy un agente y tengo 1 de riqueza!

Intercambio entre Agentes¶

Volviendo al MoneyAgent, ahora se va a crear el proceso real de intercambio.

Contexto:
Aquí es donde se define el comportamiento del agente en cada paso o step del modelo.

Información específica del modelo:
En este caso, el agente verificará su riqueza y, si tiene dinero, regalará una unidad a otro agente aleatorio.

Implementación del código:

  • El método step del agente es llamado por mesa.Agent.shuffle_do("exchange") en cada paso del modelo.

  • Para permitir que el agente elija a otro agente de manera aleatoria, utilizamos el generador de números aleatorios model.random.

  • Este funciona de la misma manera que el módulo random de Python, pero si se establece una semilla fija al instanciar el modelo (ver desafío anterior), esto permite a los usuarios replicar una ejecución específica del modelo más adelante.

  • Una vez que identificamos a este otro agente, aumentamos su riqueza en 1 y reducimos la riqueza del agente actual en 1.

In [36]:
class MoneyAgent(mesa.Agent):
    """Un agente con riqueza inicial fija."""

    def __init__(self, model):
        # Pasar los parámetros a la clase padre.
        super().__init__(model)

        # Crear la variable del agente y establecer los valores iniciales.
        self.wealth = 1

    def exchange(self):
        # Verificar que el agente tenga algo de riqueza.
        if self.wealth > 0:
            other_agent = self.random.choice(self.model.agents)
            if other_agent is not None:
                other_agent.wealth += 1
                self.wealth -= 1
In [37]:
class MoneyModel(mesa.Model):
    """Un modelo con un cierto número de agentes."""

    def __init__(self, n):
        super().__init__()
        self.num_agents = n

        # Crear los agentes.
        MoneyAgent.create_agents(model=self, n=n)

    def step(self):
        """Avanzar el modelo un paso."""
        # Esta función reorganiza pseudoaleatoriamente la lista de objetos agente y
        # luego itera llamando la función pasada como parámetro.
        self.agents.shuffle_do("exchange")

Ejecutando tu primer modelo¶

Con el comportamiento de intercambio agregado, es momento de ejecutar la primera versión rudimentaria del modelo.

Ahora, creemos un modelo con 10 agentes y ejecutémoslo durante 30 pasos.

In [38]:
model = MoneyModel(10)  # Indica al modelo que cree 10 agentes
for _ in range(30):  # Ejecuta el modelo durante 30 pasos
    model.step()

# Nota: Un guion bajo (_) es una convención común para una variable que no se usa.

  • Necesitamos extraer algunos datos del modelo.

  • Específicamente, queremos ver la distribución de la riqueza de los agentes.

In [39]:
agent_wealth = [a.wealth for a in model.agents]

# Crear un histograma con Seaborn
g = sns.histplot(agent_wealth, discrete=True)

g.set(title="Distribución de riqueza", xlabel="Riqueza", ylabel="Número de agentes");
No description has been provided for this image

  • Para tener una mejor idea de cómo se comporta un modelo, podemos crear múltiples objetos de modelo y observar la distribución que emerge de todos ellos.

  • Podemos hacer esto con un bucle for anidado:

In [40]:
all_wealth = []

# Esto ejecuta el modelo 100 veces, cada modelo ejecutando 30 pasos sobre 10 agentes
for _ in range(100):
    # Ejecutar el modelo
    model = MoneyModel(10)
    for _ in range(30):
        model.step()

    # Almacenar los resultados
    for agent in model.agents:
        all_wealth.append(agent.wealth)
In [41]:
# Usar Seaborn
g = sns.histplot(all_wealth, discrete=True)
g.set(title="Distribución de riqueza", xlabel="Riqueza", ylabel="Número de agentes");
No description has been provided for this image

  • Esto ejecuta 100 instancias del modelo, y ejecuta cada una durante 30 pasos.

  • Observa que configuramos los bins del histograma como números enteros (discrete=True), ya que los agentes solo pueden tener cantidades enteras de riqueza.

  • Esta distribución se ve mucho más suave. Al ejecutar el modelo 100 veces, suavizamos algo del 'ruido' de la aleatoriedad y llegamos al comportamiento esperado general del modelo.

  • A pesar de que todos los agentes, en promedio, dan y reciben una unidad de dinero en cada paso, el modelo converge a un estado en el que la mayoría de los agentes tiene una pequeña cantidad de dinero y un pequeño número tiene mucho dinero.

Agregar la dimensión espacial¶

Contexto: Muchos ABMs tienen un elemento espacial, con agentes moviéndose y interactuando con vecinos cercanos. Las rejillas de Mesa se dividen en celdas, y los agentes solo pueden estar en una celda en particular, como piezas en un tablero de ajedrez.

Mesa tiene dos tipos principales de rejillas: SingleGrid y MultiGrid.

  • SingleGrid permite como máximo un agente por celda;
  • MultiGrid permite que múltiples agentes estén en la misma celda.

Vamos a usar MultiGrid y luego solo intercambiaremos dinero con agentes en la misma celda.

Información específica del modelo:

  • Vamos a colocar a nuestros agentes en una rejilla y hacerlos caminar de manera aleatoria.

  • En lugar de dar su unidad de dinero a cualquier agente aleatorio, se lo darán a un agente en la misma celda.

Implementación del código:

  • Obtenemos un número entero aleatorio dentro del ancho y alto del espacio de la rejilla y usamos la función place_agent del multigrid de Mesa para colocar al agente en la ubicación de la rejilla especificada.

  • Iniciamos una rejilla con parámetros de ancho y alto, y un valor booleano que indica si la rejilla es toroidal.

  • Podemos colocar agentes en una rejilla con el método place_agent de la rejilla, que toma un agente y una tupla (x, y) de las coordenadas para colocar al agente.

In [42]:
class MoneyModel(mesa.Model):
    """Un modelo con una cantidad de agentes."""

    def __init__(self, n, width, height, seed=None):
        super().__init__(seed=seed)
        self.num_agents = n
        self.grid = mesa.space.MultiGrid(width, height, True)

        # Crear agentes
        agents = MoneyAgent.create_agents(model=self, n=n)
        
        # Crear posiciones x e y para los agentes
        x = self.rng.integers(0, self.grid.width, size=(n,))
        y = self.rng.integers(0, self.grid.height, size=(n,))
        for a, i, j in zip(agents, x, y):
            # Colocar al agente en una celda aleatoria de la rejilla
            self.grid.place_agent(a, (i, j))

Movimiento en Mesa¶

  • El agente está contenido en la celda y tiene una variable pos con una tupla de coordenadas (x, y). El método place_agent agrega automáticamente la coordenada al agente.

  • Mesa tiene un método incorporado llamado get_neighborhood, que devuelve todos los vecinos de una celda dada. Este método puede obtener dos tipos de vecindarios de celdas: Moore (incluye las 8 casillas circundantes) y Von Neumann (solo arriba/abajo/izquierda/derecha).

In [43]:
class MoneyAgent(mesa.Agent):
    def move(self):
        possible_steps = self.model.grid.get_neighborhood(
            self.pos,
            moore=True,
            include_center=False)
        new_position = self.random.choice(possible_steps)
        self.model.grid.move_agent(self, new_position)

  • A continuación, necesitamos obtener todos los demás agentes presentes en una celda y darle algo de dinero a uno de ellos.

  • Podemos obtener el contenido de una o más celdas utilizando el método get_cell_list_contents de la rejilla, o accediendo directamente a una celda.

  • El método acepta una lista de tuplas de coordenadas de celdas, o una sola tupla si solo nos interesa una celda.

In [44]:
class MoneyAgent(mesa.Agent):
    def give_money(self):
        cellmates = self.model.grid.get_cell_list_contents([self.pos])
        # Asegurar que el agente no intercambia dinero consigo mismo
        cellmates.pop(
            cellmates.index(self)
        )
        if len(cellmates) > 0:
            other = self.random.choice(cellmates)
            other.wealth += 1
            self.wealth -= 1

Ahora, juntando todo esto debería verse así:

In [45]:
class MoneyAgent(mesa.Agent):
    """Un Agente con una cantidad fija de riqueza inicial"""

    def __init__(self, model):
        super().__init__(model)
        self.wealth = 1

    def move(self):
        possible_steps = self.model.grid.get_neighborhood(
            self.pos, moore=True, include_center=False
        )
        new_position = self.random.choice(possible_steps)
        self.model.grid.move_agent(self, new_position)

    def give_money(self):
        cellmates = self.model.grid.get_cell_list_contents([self.pos])
        # Asegurar que el agente no intercambia dinero consigo mismo
        cellmates.pop(cellmates.index(self))
        if len(cellmates) > 0:
            other_agent = self.random.choice(cellmates)
            other_agent.wealth += 1
            self.wealth -= 1
In [46]:
class MoneyModel(mesa.Model):
    """Un modelo con una cantidad de agentes."""

    def __init__(self, n, width, height, seed=None):
        super().__init__(seed=seed)
        self.num_agents = n
        self.grid = mesa.space.MultiGrid(width, height, True)

        # Creamos los agentes
        agents = MoneyAgent.create_agents(model=self, n=n)
        # Creamos las coordenadas (x,y) para los agentes
        x = self.rng.integers(0, self.grid.width, size=(n,))
        y = self.rng.integers(0, self.grid.height, size=(n,))
        for a, i, j in zip(agents, x, y):
            # Añadimos el agenta a una celda aleatoria dentro de la malla
            self.grid.place_agent(a, (i, j))

    def step(self):
        self.agents.shuffle_do("move")
        self.agents.do("give_money")

Creemos un modelo con 100 agentes en una cuadrícula de 10x10 y ejecutémoslo durante 20 pasos.

In [55]:
model = MoneyModel(1000, 50, 50)
for _ in range(20):
    model.step()
  • Ahora usemos seaborn y numpy para visualizar el número de agentes que residen en cada celda.
  • Para ello, creamos un array numpy del mismo tamaño que la cuadrícula, lleno de ceros.
  • Luego, usamos la función coord_iter() del objeto de la cuadrícula, que nos permite recorrer cada celda de la cuadrícula, obteniendo la posición y el contenido de cada una.
In [56]:
agent_counts = np.zeros((model.grid.width, model.grid.height))
for cell_content, (x, y) in model.grid.coord_iter():
    agent_count = len(cell_content)
    agent_counts[x][y] = agent_count
In [57]:
g = sns.heatmap(agent_counts, cmap="viridis", annot=False, cbar=True, square=True)
g.figure.set_size_inches(5, 5)
g.set(title="Número de agentes en cada celda de la red");
No description has been provided for this image

Actividad:¶

  • Modifica el tamaño de la cuadricula

Recopilación de Datos¶

  • Dado que uno de los principales objetivos de los modelos basados en agentes es generar datos para su análisis, Mesa proporciona una clase que puede manejar la recopilación y almacenamiento de datos para nosotros, facilitando su análisis.

El recopilador de datos almacena tres categorías de datos:

  • Variables a nivel de modelo: Las funciones de recopilación a nivel de modelo toman un objeto modelo como entrada. Por ejemplo, una función que calcula una dinámica del modelo completo (coeficiente de Gini).
  • Variables a nivel de agente: Las funciones de recopilación a nivel de agente toman un objeto agente como entrada y generalmente son el estado de los atributos del agente, en este caso la riqueza.
  • Tablas (que son un recipiente para todo lo demás).

Información específica del modelo:

  • A nivel de modelo, mediremos el Coeficiente de Gini del modelo, una medida de la desigualdad de riqueza.

  • A nivel de agente, queremos recopilar la riqueza de cada agente en cada paso.

La función compute_gini calcula el estimador muestral del Coeficiente de Gini:

$ G = 1 + \frac{1}{n} - 2 \cdot B $

donde:

$ B = \frac{\sum_{i=1}^{n} x_i \cdot (n - i)}{n \cdot \sum_{i=1}^{n} x_i},\quad x_1 < x_2 < ... < x_n $

Este valor de (B) es la suma ponderada de las riquezas multiplicadas por la cantidad de agentes que tienen una riqueza mayor o igual que el agente (i), normalizada por el total de la riqueza y el número total de agentes.

  • Gini, Corrado (1936)
  • Dixon, P. M.; Weiner, J.; Mitchell-Olds, T.; and Woodley, R. (1988).
In [58]:
def compute_gini(model):
    agent_wealths = [agent.wealth for agent in model.agents]
    x = sorted(agent_wealths)
    n = model.num_agents
    B = sum(xi * (n - i) for i, xi in enumerate(x)) / (n * sum(x))
    return (1 + (1 / n) - 2 * B)

Implementación del código:

  • Vamos a agregar un DataCollector al modelo con mesa.DataCollector, y recopilaremos la riqueza de los agentes y el coeficiente de Gini en cada paso de tiempo.
In [59]:
class MoneyAgent(mesa.Agent):
    """Un Agente con una cantidad fija de riqueza inicial"""

    def __init__(self, model):
        super().__init__(model)
        self.wealth = 1

    def move(self):
        possible_steps = self.model.grid.get_neighborhood(
            self.pos, moore=True, include_center=False
        )
        new_position = self.random.choice(possible_steps)
        self.model.grid.move_agent(self, new_position)

    def give_money(self):
        cellmates = self.model.grid.get_cell_list_contents([self.pos])
        # Nos aseguramos que el agente no intercambie dinero consigo mismo
        cellmates.pop(cellmates.index(self))
        if len(cellmates) > 0:
            other = self.random.choice(cellmates)
            other.wealth += 1
            self.wealth -= 1
In [60]:
class MoneyModel(mesa.Model):
    """Un modelo con una cantidad de agentes."""

    def __init__(self, n, width, height):
        super().__init__()
        self.num_agents = n
        # Creamos el espacio
        self.grid = mesa.space.MultiGrid(width, height, True)
        # Recolectamos la salida
        self.datacollector = mesa.DataCollector(
            model_reporters={"Gini": compute_gini}, agent_reporters={"Riqueza": "wealth"}
        )

        # Creamos los agentes
        agents = MoneyAgent.create_agents(model=self, n=n)
        # Creamos las posiciones (x,y) de los agentes
        x = self.rng.integers(0, self.grid.width, size=(n,))
        y = self.rng.integers(0, self.grid.height, size=(n,))
        for a, i, j in zip(agents, x, y):
            # Añadimos el agente a una celda aleatoria
            self.grid.place_agent(a, (i, j))

    def step(self):
        self.datacollector.collect(self)
        self.agents.shuffle_do("move")
        self.agents.do("give_money")

En cada paso del modelo, el recopilador de datos recopilará y almacenará el coeficiente de Gini actual a nivel de modelo, así como la riqueza de cada agente, asociándolos con el paso actual.

In [61]:
model = MoneyModel(100, 10, 10)
for _ in range(100):
    model.step()

Visualización de datos de un modelo¶

In [62]:
gini = model.datacollector.get_model_vars_dataframe()
# Graficar el coeficiente de Gini a través del tiempo
g = sns.lineplot(data=gini)
g.set(title="Gini Coefficient over Time", ylabel="Gini Coefficient");
No description has been provided for this image

Visualización de datos de un agente¶

In [63]:
agent_wealth = model.datacollector.get_agent_vars_dataframe()
agent_wealth
Out[63]:
Riqueza
Step AgentID
1 1 1
2 1
3 1
4 1
5 1
... ... ...
100 96 2
97 3
98 -4
99 -1
100 1

10000 rows × 1 columns

  • El índice del DataFrame está formado por pares de pasos del modelo e ID del agente.
  • Esto se debe a que el recopilador de datos almacena los datos en un diccionario, con el número de paso como clave y un diccionario de pares de ID del agente y valor de variable como valor.
  • El recopilador de datos convierte este diccionario en un DataFrame, por lo que el índice es un par de (paso del modelo, ID del agente).
  • Puede analizarlo como cualquier otro DataFrame.
  • Por ejemplo, para obtener un histograma de la riqueza del agente al final del modelo
In [64]:
last_step = agent_wealth.index.get_level_values("Step").max()
end_wealth = agent_wealth.xs(last_step, level="Step")["Riqueza"]

# Crear un histograma de la riqueza en el último paso
g = sns.histplot(end_wealth, discrete=True)
g.set(
    title="Distribución de la riqueza en el último paso",
    xlabel="Riqueza",ylabel="Número de Agentes");
No description has been provided for this image

Para representar gráficamente la riqueza de un agente determinado (en este ejemplo, el agente 7):

In [65]:
# Obtener la riqueza del agente 7 a través del tiempo
one_agent_wealth = agent_wealth.xs(7, level="AgentID")

# Graficar la riqueza del agente 7 a través del tiempo
g = sns.lineplot(data=one_agent_wealth, x="Step", y="Riqueza")
g.set(title="Riqueza del agente 7 a través del tiempo");
No description has been provided for this image

Es posible graficar el comportamiento de múltiples agentes a lo largo del tiempo.

In [38]:
agent_list = [3, 14, 25]

# Obtener la riqueza de múltiples agentes a través del tiempo
multiple_agents_wealth = agent_wealth[
    agent_wealth.index.get_level_values("AgentID").isin(agent_list)
]
# Graficar la riqueza de múltiples agentes a través del tiempo
g = sns.lineplot(data=multiple_agents_wealth, x="Step", y="Riqueza", hue="AgentID")
g.set(title="Riqueza de agentes 3, 14 y 25 a través del tiempo");
No description has been provided for this image

Incluso podemos graficar el promedio de todos los agentes, con un intervalo de confianza del 95% para ese promedio.

In [39]:
# Transformar los datos a un formato largo
agent_wealth_long = agent_wealth.T.unstack().reset_index()
agent_wealth_long.columns = ["Step", "AgentID", "Variable", "Value"]
agent_wealth_long.head(3)

# Graficar la riqueza promedio a través del tiempo
g = sns.lineplot(data=agent_wealth_long, x="Step", y="Value", errorbar=("ci", 95))
g.set(title="Riqueza promedio")
Out[39]:
[Text(0.5, 1.0, 'Riqueza promedio')]
No description has been provided for this image

Lo cual es exactamente 1, como se esperaba en este modelo, ya que cada agente comienza con una unidad de riqueza y cada agente le da una unidad de riqueza a otro agente en cada paso.

  • También puede usar Pandas para exportar los datos a un archivo CSV (valores separados por comas), que puede abrirse con cualquier aplicación de hoja de cálculo común o con Pandas.

  • Si no especifica una ruta de archivo, este se guardará en el directorio local.

In [40]:
# guardar los datos del modelo (almacenados en el objeto gini de pandas) en CSV
gini.to_csv("model_data.csv")

# guardar los datos del agente (almacenados en el objeto pandas agent_wealth) en CSV
agent_wealth.to_csv("agent_data.csv")

Ejercicio¶

Modifica la clase MoneyAgent para que los agentes no tengan deuda

Solución¶

In [66]:
class MoneyAgent(mesa.Agent):
    """Un Agente con una cantidad fija de riqueza inicial"""

    def __init__(self, model):
        super().__init__(model)
        self.wealth = 1

    def move(self):
        possible_steps = self.model.grid.get_neighborhood(
            self.pos, moore=True, include_center=False
        )
        new_position = self.random.choice(possible_steps)
        self.model.grid.move_agent(self, new_position)

    def give_money(self):
        cellmates = self.model.grid.get_cell_list_contents([self.pos])
        # Nos aseguramos que el agente no intercambie dinero consigo mismo
        cellmates.pop(cellmates.index(self))
        if (len(cellmates)> 0) and (self.wealth > 0):
            other = self.random.choice(cellmates)
            other.wealth += 1
            self.wealth -= 1
In [67]:
model = MoneyModel(100, 10, 10)
for _ in range(100):
    model.step()
In [68]:
gini = model.datacollector.get_model_vars_dataframe()
# Graficar el coeficiente de Gini a través del tiempo
g = sns.lineplot(data=gini)
g.set(title="Gini Coefficient over Time", ylabel="Gini Coefficient");
No description has been provided for this image
In [69]:
agent_wealth = model.datacollector.get_agent_vars_dataframe()
agent_wealth
Out[69]:
Riqueza
Step AgentID
1 1 1
2 1
3 1
4 1
5 1
... ... ...
100 96 0
97 0
98 0
99 0
100 1

10000 rows × 1 columns

In [70]:
last_step = agent_wealth.index.get_level_values("Step").max()
end_wealth = agent_wealth.xs(last_step, level="Step")["Riqueza"]

# Crear un histograma de la riqueza en el último paso
g = sns.histplot(end_wealth, discrete=True)
g.set(title="Distribución de la riqueza en el último paso",
    xlabel="Riqueza",ylabel="Número de Agentes");
No description has been provided for this image

Gestión de Agentes a Través de AgentSet¶

Contexto:

  • Mesa utiliza AgentSet, para permitir a los usuarios gestionar sus agentes de manera eficiente e intuitiva.

Información específica del modelo: Mostraremos dos técnicas de gestión de agentes solo para demostrar su capacidad:

  1. Selección: Estableceremos una política en la que los agentes ricos den dinero a los agentes pobres.
  2. Agrupar: Agruparemos a los agentes según su riqueza.

Selección¶

Información específica del modelo: Para esta variación del modelo, implementaremos una política según la cual los agentes ricos otorgarán dinero a los agentes pobres.

Implementación del código: Usaremos agents.select para separar los agentes en ricos y pobres. Si hay agentes ricos, serán los únicos que otorgarán dinero.

In [73]:
class MoneyAgent(mesa.Agent):
    """Agente con riqueza inicial fija"""

    def __init__(self, model):
        super().__init__(model)
        self.wealth = 1

    def give_money(self, poor_agents):
        if self.wealth > 0:
            other_agent = self.random.choice(poor_agents)
            other_agent.wealth += 1
            self.wealth -= 1
In [78]:
class MoneyModel(mesa.Model):
    """Modelo con un número de agentes ."""

    def __init__(self, n):
        super().__init__()
        self.num_agents = n

        # Crear agentes
        MoneyAgent.create_agents(model=self, n=n)

        self.datacollector = mesa.DataCollector(
            model_reporters={"Gini": compute_gini}, agent_reporters={"Wealth": "wealth"}
        )

    def step(self):
        self.datacollector.collect(self)
        # Obtener lista de agentes ricos y pobres
        rich_agents = model.agents.select(lambda a: a.wealth >= 2)
        poor_agents = model.agents.select(lambda a: a.wealth < 2)
        # Cuando hay agentes ricos, solo les dan dinero a los agentes pobres.
        if len(rich_agents) > 0:
            rich_agents.shuffle_do("give_money", poor_agents)
        else:
            poor_agents.shuffle_do("give_money", poor_agents)

Ahora ejecutamos el modelo, recopilamos los datos y graficamos los resultados.

In [79]:
model = MoneyModel(100)
for _ in range(20):
    model.step()

data = model.datacollector.get_agent_vars_dataframe()
# Usamos seaborn
g = sns.histplot(data["Wealth"], discrete=True)
g.set(title="Distribución de riqueza", xlabel="Riqueza", ylabel="Número de Agentes");
No description has been provided for this image

Agrupar¶

Implementación específica del modelo: En este caso, asignaremos a los agentes un atributo de etnia: Verde, Azul o Mixto. Los agentes Verde y Azul solo donan dinero a su etnia, mientras que Mixto puede donar dinero a cualquiera.

Implementación de código: Usando groupby, ejecutaremos la lógica anterior en nuestro código pasando una lista de agentes agrupados a nuestra función give_money. Para asegurarnos de que podamos representar la riqueza por grupo, también necesitamos agregar la etnia a nuestro recopilador de datos.

In [82]:
class MoneyAgent(mesa.Agent):
    """Agente con riqueza inicial fija."""

    def __init__(self, model, ethnicity):
        super().__init__(model)
        self.wealth = 1
        self.ethnicity = ethnicity

    def give_money(self, similars):
        if self.wealth > 0:
            other_agent = self.random.choice(similars)
            other_agent.wealth += 1
            self.wealth -= 1
In [83]:
class MoneyModel(mesa.Model):
    """Modelo con un numero de agentes."""
    def __init__(self, n):
        super().__init__()
        self.num_agents = n
        # Crear lista de etnias distintas
        ethnicities = ["Green", "Blue", "Mixed"]
        for i in range(n):
            ethnicity = self.random.choice(ethnicities)
            agent = MoneyAgent(self, ethnicity)
            self.agents.add(agent)
        self.datacollector = mesa.DataCollector(
            model_reporters={"Gini": compute_gini},
            agent_reporters={"Riqueza": "wealth", "Etnia": "ethnicity"})

    def step(self):
        self.datacollector.collect(self)
        # groupby devuelve un diccionario de: 
            # clave: etnia 
            # Valor: lista de agentes con esa etnia
        grouped_agents = model.agents.groupby("ethnicity")
        for ethnic, similars in grouped_agents:
            if ethnic != "Mixed":
                similars.shuffle_do("give_money", similars)
            else:  # Esto permite que los mixtos puedan comerciar con cualquier persona.
                similars.shuffle_do("give_money", self.agents)
In [84]:
import seaborn as sns
import matplotlib.pyplot as plt

# Ejecutamos el modelo
model = MoneyModel(100)
for _ in range(20):
    model.step()

# Obtenemos los datos
data = model.datacollector.get_agent_vars_dataframe()
latest_step = data.index.get_level_values(0).max()
latest_data = data.loc[latest_step]  # Solo la última iteración
In [85]:
# Asignamos colores
palette = {"Green": "green", "Blue": "blue", "Mixed": "purple"}

# Graficamos
plt.figure(figsize=(6, 4))
g = sns.histplot(data=latest_data,x="Riqueza",hue="Etnia",
    multiple="stack",discrete=True,palette=palette,shrink=0.8)

g.set(title="Distribución de la riqueza por etnia",
    xlabel="Riqueza",
    ylabel="Número de agentes");
No description has been provided for this image

Ejecución en Lote (Batch Run)¶

  • Normalmente no ejecutarás un modelo solo una vez, sino múltiples veces, con parámetros fijos para encontrar las distribuciones que genera el modelo, y con parámetros variables para analizar cómo estos afectan las salidas y comportamientos del modelo.

  • A esto se le conoce comúnmente como barrido de parámetros (parameter sweeps).

  • En lugar de tener que escribir bucles anidados para cada ejecución del modelo, Mesa proporciona una función llamada batch_run, la cual automatiza este proceso por ti.

Reporte adicional del agente¶

  • Para hacer los resultados un poco más interesantes, también vamos a calcular el número de pasos de tiempo consecutivos en los que un agente no ha entregado ninguna riqueza, utilizando un reporte de agente (agent reporter).

  • De esta manera, podemos observar cómo se maneja la información cuando se utilizan múltiples reportes en el modelo.

In [91]:
class MoneyModel(mesa.Model):
    """A model with some number of agents."""

    def __init__(self, n, width, height, seed=None):
        super().__init__(seed=seed)
        self.num_agents = n
        self.grid = mesa.space.MultiGrid(width, height, True)
        self.running = True

        # Crear agentes
        agents = MoneyAgent.create_agents(model=self, n=n)
        # Create x and y positions for agents
        x = self.rng.integers(0, self.grid.width, size=(n,))
        y = self.rng.integers(0, self.grid.height, size=(n,))
        for a, i, j in zip(agents, x, y):
            # Asignar agente a una celda aleatoria
            self.grid.place_agent(a, (i, j))

        self.datacollector = mesa.DataCollector(
            model_reporters={"Gini": compute_gini},
            agent_reporters={"Wealth": "wealth", "Steps_not_given": "steps_not_given"})

    def step(self):
        self.datacollector.collect(self)
        self.agents.shuffle_do("move")
        self.agents.shuffle_do("give_money")
In [93]:
class MoneyAgent(mesa.Agent):
    """An agent with fixed initial wealth."""

    def __init__(self, model):
        super().__init__(model)
        self.wealth = 1
        self.steps_not_given = 0

    def move(self):
        possible_steps = self.model.grid.get_neighborhood(
            self.pos, moore=True, include_center=False
        )
        new_position = self.random.choice(possible_steps)
        self.model.grid.move_agent(self, new_position)

    def give_money(self):
        cellmates = self.model.grid.get_cell_list_contents([self.pos])
        cellmates.pop(cellmates.index(self))
        if len(cellmates) > 0 and self.wealth > 0:
            other = self.random.choice(cellmates)
            other.wealth += 1
            self.wealth -= 1
            self.steps_not_given = 0
        else:
            self.steps_not_given += 1

Parámetros de ejecución en lote (Batch Run)¶

Llamamos a batch_run con los siguientes argumentos:

  • model_cls
    La clase del modelo que se utilizará para la ejecución en lote.

  • parameters
    Un diccionario que contiene todos los parámetros de la clase del modelo y los valores deseados para usar en la ejecución en lote como pares clave-valor. Cada valor puede ser fijo (por ejemplo, {"height": 10, "width": 10}) o un iterable (por ejemplo, {"n": range(10, 500, 10)}).

batch_run generará todas las combinaciones posibles de parámetros basadas en este diccionario y ejecutará el modelo iterations veces por cada combinación.

  • number_processes
    Si no se especifica, el valor predeterminado es 1. Puedes establecerlo como None para usar todos los procesadores disponibles.
    Nota: El uso de multiprocesamiento puede dificultar la depuración. Si tus barridos de parámetros están arrojando errores inesperados, establece number_processes=1.

  • iterations
    El número de iteraciones que se ejecutarán por cada combinación de parámetros. Opcional. Si no se especifica, el valor predeterminado es 1.

  • data_collection_period
    La duración del período (en número de pasos) después del cual se recolectan los datos del modelo y de los agentes. Opcional. Si no se especifica, el valor predeterminado es -1, es decir, solo al final de cada episodio.

  • max_steps
    El número máximo de pasos de tiempo después del cual el modelo se detiene. Un episodio termina cuando self.running del modelo se establece en False, o cuando model.steps == max_steps. Opcional. Si no se especifica, el valor predeterminado es 1000.

  • display_progress
    Muestra el progreso de la ejecución en lote. Opcional. Si no se especifica, el valor predeterminado es True.

En el siguiente ejemplo, mantenemos fija la altura y el ancho, y variamos el número de agentes. Indicamos al batch runner que ejecute 5 instancias del modelo con cada cantidad de agentes, y que cada una se ejecute por 100 pasos de tiempo.

Queremos hacer seguimiento de:

  1. El valor del coeficiente de Gini en cada paso de tiempo.
  2. El desarrollo de la riqueza individual de los agentes y los pasos sin entregar dinero.

Importante: Para este segundo punto, como los cambios en cada paso de tiempo pueden ser interesantes, configuramos data_collection_period=1. Por defecto, los datos solo se recopilan al final de cada episodio.

Nota: El número total de ejecuciones es 245 (49 diferentes tamaños de población * 5 iteraciones por tamaño). Sin embargo, la lista resultante de diccionarios tendrá una longitud de 6,186,250
(250 agentes promedio por población * 49 poblaciones * 5 iteraciones * 101 pasos por iteración).

In [94]:
params = {"width": 10, "height": 10, "n": range(5, 100, 5)}
params
Out[94]:
{'width': 10, 'height': 10, 'n': range(5, 100, 5)}
In [95]:
# Ejecutamos el batch run con los parámetros especificados
results = mesa.batch_run(
    MoneyModel,               # El modelo que se va a ejecutar
    parameters=params,        # Los parámetros del modelo
    iterations=5,             # Número de iteraciones por cada combinación de parámetros
    max_steps=100,            # Número máximo de pasos de tiempo por ejecución
    number_processes=1,       # Número de procesos a usar (1 en este caso)
    data_collection_period=1, # Período de recolección de datos (1 paso de tiempo)
    display_progress=True,    # Mostrar el progreso de la ejecución
)

100%|██████████| 95/95 [00:03<00:00, 28.34it/s]

Análisis y Visualización de la Ejecución por Lotes¶

Para analizar más a fondo el retorno de la función batch_run, convertimos la lista de diccionarios a un DataFrame de Pandas y mostramos sus claves.

In [96]:
results_df = pd.DataFrame(results)
print(results_df.keys())

Index(['RunId', 'iteration', 'Step', 'width', 'height', 'n', 'Gini', 'AgentID',
       'Wealth', 'Steps_not_given'],
      dtype='object')

  • Primero, queremos examinar más de cerca cómo cambia el coeficiente de Gini al final de cada episodio a medida que aumentamos el tamaño de la población.

  • Para esto, filtramos nuestros resultados para que solo contengan los datos de un agente (el coeficiente de Gini será el mismo para toda la población en cualquier momento) en el paso 100 de cada episodio y luego representamos gráficamente los valores del coeficiente de Gini en función del número de agentes.

  • Ten en cuenta que hay cinco valores para cada tamaño de población, ya que configuramos iterations=5 al llamar a la ejecución por lotes.

In [97]:
# Filtrar los resultados para contener solo los datos de un agente
# El coeficiente de Gini será el mismo para toda la población en cualquier momento
results_filtered = results_df[(results_df.AgentID == 1) & (results_df.Step == 100)]
results_filtered[["iteration", "n", "Gini"]].reset_index(
    drop=True
).head()  # Crear un gráfico de dispersión
Out[97]:
iteration n Gini
0 0 5 0.000000
1 0 10 0.180000
2 0 15 0.124444
3 0 20 0.265000
4 0 25 0.278400
In [98]:
g = sns.scatterplot(data=results_filtered, x="n", y="Gini")
g.set(xlabel="número de agentes",
    ylabel="coeficiente de Gini",
    title="Coeficiente de Gini vs. número de agentes")
Out[98]:
[Text(0.5, 0, 'número de agentes'),
 Text(0, 0.5, 'coeficiente de Gini'),
 Text(0.5, 1.0, 'Coeficiente de Gini vs. número de agentes')]
No description has been provided for this image

Podemos crear diferentes tipos de gráficos a partir de este DataFrame filtrado. Por ejemplo, un gráfico de puntos con barras de error.

In [99]:
# Crear un gráfico de puntos con barras de error
g = sns.pointplot(data=results_filtered, x="n", y="Gini", linestyle="None")
g.figure.set_size_inches(8, 4)
g.set(xlabel="número de agentes",ylabel="coeficiente de Gini",
    title="Coeficiente de Gini vs. número de agentes")
Out[99]:
[Text(0.5, 0, 'número de agentes'),
 Text(0, 0.5, 'coeficiente de Gini'),
 Text(0.5, 1.0, 'Coeficiente de Gini vs. número de agentes')]
No description has been provided for this image

Analizando reportes del modelo: Comparando 5 escenarios¶

  • Se pueden obtener otros hallazgos al comparar el coeficiente de Gini de diferentes escenarios.

  • Por ejemplo, podemos comparar el coeficiente de Gini de una población con 25 agentes con el de una población con 400 agentes.

  • Para ello, aumentamos el número de iteraciones a 25, con el fin de obtener una mejor estimación del coeficiente de Gini para cada tamaño de población y obtener estimaciones útiles de error.

  • Al observar cómo varía el modelo según los parámetros, es importante destacar nuevamente que los usuarios pueden establecer una semilla aleatoria.

  • Debido a la aleatoriedad inherente en muchos modelos basados en agentes (ABMs), la semilla es crucial para:

  • Reproducibilidad: Poder replicar los resultados del modelo ABM.

  • Análisis de sensibilidad: Identificar qué tan sensibles o robustos son los resultados del modelo frente a fluctuaciones aleatorias.

Tratar la semilla como un parámetro adicional y ejecutar numerosos escenarios nos permite ver el impacto de la aleatoriedad en este modelo.

In [100]:
params = {"seed": None, "width": 10, "height": 10, "n": [5, 10, 20, 40, 80]}

results_5s = mesa.batch_run(
    MoneyModel,
    parameters=params,
    iterations=25,
    max_steps=100,
    number_processes=1,
    data_collection_period=1,  # Need to collect every step
    display_progress=True,
)

results_5s_df = pd.DataFrame(results_5s)

100%|██████████| 125/125 [00:03<00:00, 40.37it/s]

  • Filtramos nuevamente los resultados para que solo contengan los datos de un agente.

  • El coeficiente de Gini será el mismo para toda la población en cualquier momento.

In [101]:
results_5s_df_filtered = results_5s_df[(results_5s_df.AgentID == 1)]
results_5s_df_filtered.head(3)
Out[101]:
RunId iteration Step seed width height n Gini AgentID Wealth Steps_not_given
1 0 0 1 None 10 10 5 0.0 1.0 1.0 0.0
6 0 0 2 None 10 10 5 0.0 1.0 1.0 1.0
11 0 0 3 None 10 10 5 0.0 1.0 1.0 2.0
In [102]:
### Crear un gráfico de líneas con barras de error
g = sns.lineplot(data=results_5s_df,x="Step",y="Gini",hue="n",errorbar=("ci", 95),palette="tab10")
g.figure.set_size_inches(8, 4)
plot_title = ("Coeficiente de Gini para distintos tamaños de población\n"
    "(promedio de 100 ejecuciones, con intervalo de confianza del 95%)")
g.set(title=plot_title, ylabel="Coeficiente de Gini");
No description has been provided for this image

En este caso, parece que el coeficiente de Gini aumenta más lentamente para poblaciones pequeñas.
Esto puede deberse a varios factores:

  • El coeficiente de Gini es una medida de desigualdad, y mientras más pequeña sea la población, mayor es la probabilidad de que todos los agentes estén en una clase de riqueza similar.

  • También puede ser que en poblaciones más pequeñas haya menos interacciones entre agentes, lo cual significa que la riqueza de un agente tiene menos probabilidad de cambiar.

Ejercicio: Tratar la semilla como un parámetro y observar su impacto en el coeficiente de Gini¶

Puedes analizar cómo la aleatoriedad afecta los resultados del modelo tratando la semilla (seed) como un parámetro adicional.

Una forma de visualizar este impacto es graficando la evolución del coeficiente de Gini con respecto al número de pasos, diferenciando por la semilla utilizada.
Para hacerlo, puedes modificar el parámetro hue en la función sns.lineplot para que agrupe los resultados según la semilla:

Solución¶

In [103]:
from mesa.batchrunner import batch_run
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt

# Definimos el rango de semillas a usar
seed_values = list(range(5))  # 5 simulaciones con diferentes semillas

# Definimos los parámetros del modelo, incluyendo la semilla como variable
params = {"seed": seed_values , "width": 10, "height": 10, "n": [5, 10, 20, 40, 80]}
In [104]:
# Ejecutamos las simulaciones
results_seed = batch_run(
    MoneyModel,
    parameters=params,
    iterations=25,
    max_steps=100,
    number_processes=1,
    data_collection_period=1,
    display_progress=True
)

100%|██████████| 625/625 [00:15<00:00, 41.02it/s]
In [105]:
# Convertimos a DataFrame
results_seed_df = pd.DataFrame(results_seed)

# Filtramos solo una instancia de agente para visualizar el Gini (es igual para todos)
results_seed_filtered = results_seed_df[results_seed_df.AgentID == 1]
In [106]:
# Graficamos el coeficiente de Gini a través del tiempo, diferenciando por semilla
sns.set(style="whitegrid")
g = sns.lineplot(data=results_seed_filtered,x="Step",y="Gini",hue="seed",palette="tab10")
g.figure.set_size_inches(10, 5)
g.set(title="Impacto de la semilla aleatoria sobre el coeficiente de Gini",
    xlabel="Paso de simulación",ylabel="Coeficiente de Gini")
plt.show()
No description has been provided for this image

Análisis de los reportes de agentes: Comparación de 5 escenarios¶

  • De los agentes hemos recolectado la riqueza y el número de rondas consecutivas sin realizar transacciones.

  • Podemos comparar los 5 tamaños de población diferentes graficando el número promedio de rondas consecutivas sin transacciones para cada tamaño poblacional.

  • Es importante notar que estamos agregando información múltiples veces: primero, calculamos el promedio de todos los agentes para cada repetición individual.

  • Luego, graficamos esos promedios de todas las repeticiones, con una banda de error que muestra el intervalo de confianza del 95% de ese primer promedio (sobre todos los agentes).

  • Por lo tanto, esta banda de error representa la incertidumbre del valor medio del número de rondas consecutivas sin transacción para cada tamaño de población.

In [108]:
# Calcular el promedio de la riqueza y el número de rondas consecutivas
# sin transacciones para todos los agentes en cada episodio.

agg_results_df = (
    results_5s_df.groupby(["iteration", "n", "Step"])
    .agg({"Wealth": "mean", "Steps_not_given": "mean"})
    .reset_index())
In [109]:
agg_results_df
Out[109]:
iteration n Step Wealth Steps_not_given
0 0 5 0 NaN NaN
1 0 5 1 1.0 0.0000
2 0 5 2 1.0 0.6000
3 0 5 3 1.0 1.2000
4 0 5 4 1.0 2.2000
... ... ... ... ... ...
12620 24 80 96 1.0 1.6125
12621 24 80 97 1.0 1.7875
12622 24 80 98 1.0 1.7625
12623 24 80 99 1.0 1.8625
12624 24 80 100 1.0 1.6625

12625 rows × 5 columns

In [110]:
# Crear un gráfico de líneas con barras de error
g = sns.lineplot(data=agg_results_df, x="Step", y="Steps_not_given", hue="n", palette="tab10")
g.figure.set_size_inches(8, 4)
g.set(title="Promedio de rondas consecutivas sin transacciones para "
    "diferentes tamaños de población\n(media con intervalo de confianza del 95%)",
    ylabel="Rondas consecutivas sin transacción")
Out[110]:
[Text(0.5, 1.0, 'Promedio de rondas consecutivas sin transacciones para diferentes tamaños de población\n(media con intervalo de confianza del 95%)'),
 Text(0, 0.5, 'Rondas consecutivas sin transacción')]
No description has been provided for this image

  • Se puede observar claramente que, a medida que disminuye el número de agentes, aumenta el número de rondas consecutivas sin una transacción.

  • Esto se debe a que los agentes tienen menos interacciones entre sí y, por lo tanto, la riqueza de un agente tiene menos probabilidades de cambiar.

Pasos generales para analizar los resultados¶

Existen muchos otros análisis posibles basados en las políticas, escenarios e incertidumbres que te interese explorar.

En general, puedes seguir estos pasos para realizar tu propio análisis:

  1. Determina las métricas que deseas analizar. Añádelas como reporteros de modelo y agente al datacollector de tu modelo.
  2. Determina los parámetros de entrada que deseas variar. Añádelos como parámetros a la función batch_run, utilizando rangos o listas para probar diferentes valores.
  1. Determina los hiperparámetros de la función batch_run. Define el número de iteraciones, el número de procesos, el número de pasos, el periodo de recolección de datos, etc.
  2. Ejecuta la función batch_run y guarda los resultados.
  3. Transforma, filtra y agrega los resultados para obtener los datos que deseas analizar.
  4. Elige el tipo de gráfico, qué mostrar en los ejes x e y, qué columnas usar para el color. Seaborn también tiene una increíble Galería de Ejemplos.
  5. Grafica los datos y analiza los resultados.

Extensiones del modelo base:¶

1. Modelo de intercambio aleatorio con propensión al ahorro¶

Un factor de propensión al ahorro λ fue introducido en el modelo de intercambio aleatorio (Chakraborti y Chakrabarti, 2000), en el cual cada agente en el tiempo t ahorra una fracción λ de su dinero $m_i(t)$ y comercia aleatoriamente con el resto:

$ m_i(t + 1) = \lambda m_i(t) + \epsilon_{ij}(1 - \lambda)(m_i(t) + m_j(t)) $ $ m_j(t + 1) = \lambda m_j(t) + (1 - \epsilon_{ij})(1 - \lambda)(m_i(t) + m_j(t)) $

donde

$ \Delta m = (1 - \lambda)\left[\epsilon_{ij}(m_i(t) + m_j(t)) - m_i(t)\right] $

y donde $\epsilon_{ij}$ es una fracción aleatoria.
Por definición, $\lambda$ es una fracción propia, es decir, $0 \leq \lambda \leq 1$.

1. Modelo de intercambio aleatorio con propensión al ahorro¶

No description has been provided for this image

Tomado de: Chakrabarti, B. K., Chakraborti, A., Chakravarty, S. R., & Chatterjee, A. (2013). Econophysics of income and wealth distributions. Cambridge University Press.

2. Modelo con deuda¶

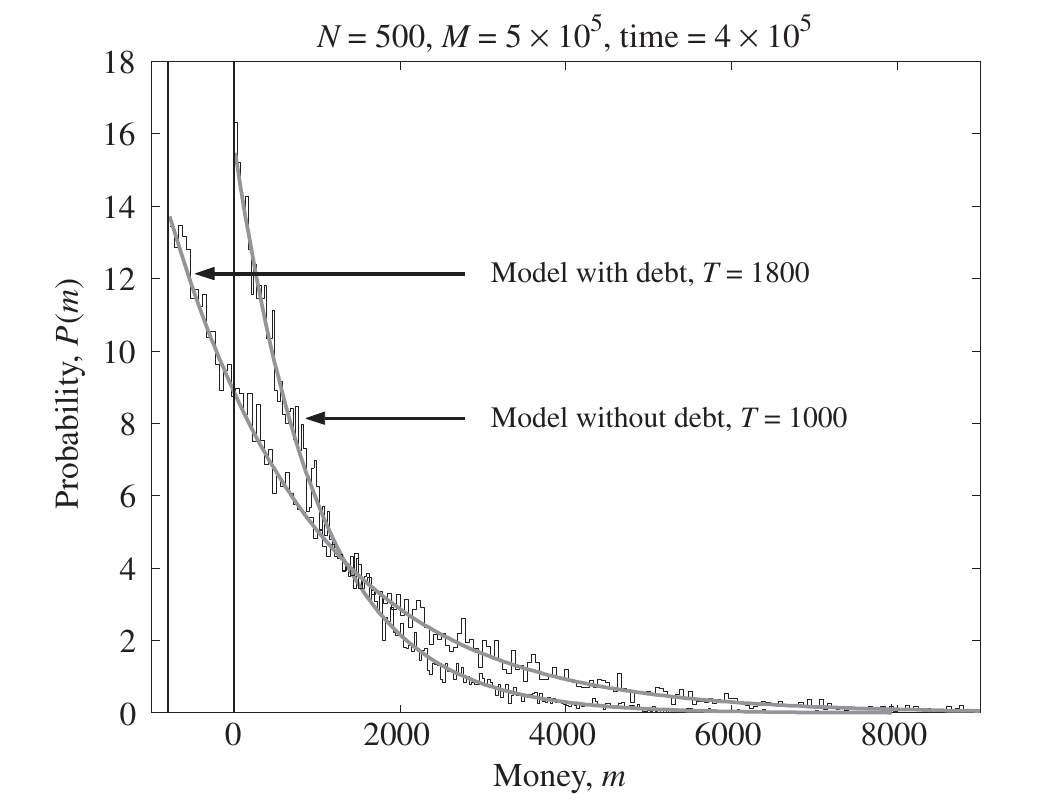
No description has been provided for this image

Tomado de: Chakrabarti, B. K., Chakraborti, A., Chakravarty, S. R., & Chatterjee, A. (2013). Econophysics of income and wealth distributions. Cambridge University Press.

3. Distribuciones generalizadas para modelar la distribución del ingreso y riqueza¶

  • McDonald, J. B., & Ransom, M. (2008). The generalized beta distribution as a model for the distribution of income: estimation of related measures of inequality. In Modeling income distributions and Lorenz curves (pp. 147-166). New York, NY: Springer New York.
  • Moghaddam, M. D., Mills, J., & Serota, R. A. (2020). From a stochastic model of economic exchange to measures of inequality. Physica A: Statistical Mechanics and its Applications, 559, 125047.
  • Clementi, F., Gallegati, M., Kaniadakis, G., & Landini, S. (2016). κ-generalized models of income and wealth distributions: A survey. The European Physical Journal Special Topics, 225, 1959-1984.

¡Gracias!¶

email: andgarm.n@gmail.com

sitio: https://sites.google.com/view/andresgm/home.